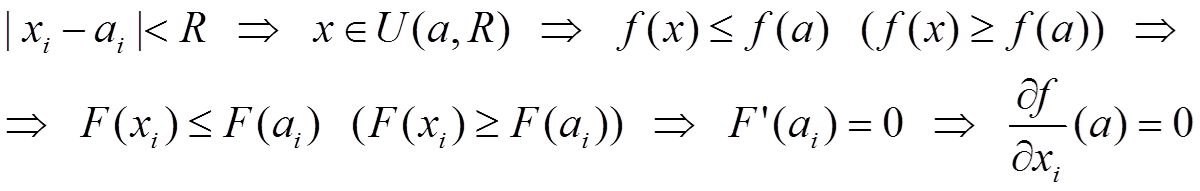Экстремумы функции

Необходимое условие экстремума

Теорема

В точке экстремума, являющейся внутренней точкой области определения, все частные производные, которые в этой точке существуют, равны нулю.

a = (a₁, ..., a_{i −1}, a_i, a_{i +1}, ..., a_n ),   x = (a₁, ..., a_{i −1}, x_i, a_{i +1}, ..., a_n ),

x ∈ U(a, R) ⇒ f(x) ≤ f(a) (f(x) ≥ f(a))

F = (x_i) = f(x) = f(a₁, a₂, ...,a_{i −1}, x_i, a_{i +1}, ..., a_n).

|x − a| = |x_i − a_i|