Производные высших порядков

Теорема

Пусть в некоторой окрестности точка x = a существуют частные производные

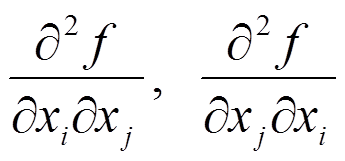
и они непрерывны в точке x = a. Тогда

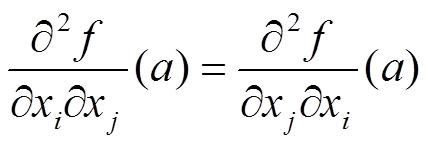
Доказательство

В последующих выкладках будут меняться только переменные x_i и x_j. Для сокращения записи обозначим их x и y, а вместо
f(x₁, x₂, …, x_n) будем писать f(x, y). Таким образом, надо проверить равенство

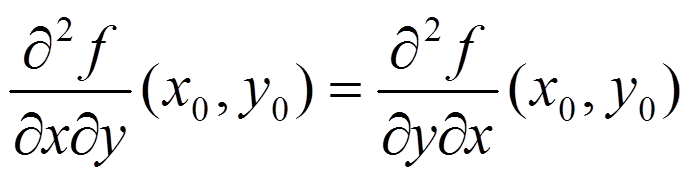
если в точке (x₀, y₀) обе части равенства непрерывны.