Разложение дроби на элементарные

Рассмотрим

.

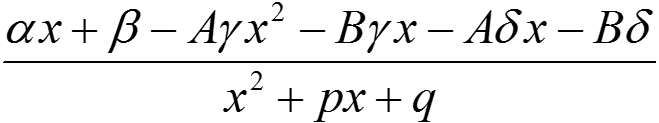Разделим числитель на знаменатель:

αx + β − Aγx² − Bγx − Aδx − Bδ = (x² + px + q)(−Aγ) + [x(α − Bγ − Aδ + Aγp) + (β − Bδ + Aγq)].

Покажем, что можно подобрать A и B так, чтобы слагаемое в квадратных скобках было равно нулю. Тогда A и B удовлетворяют системе:

.

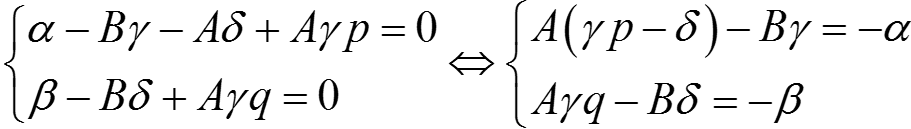
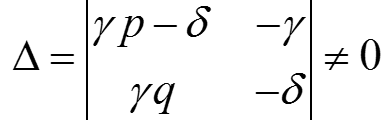Пусть Δ = −γpδ + δ² + γ²q = 0.

γ ≠ 0, так как если γ = 0, то δ = 0, а γ² + δ² > 0.

Разделим на γ² равенство −γpδ + δ² + γ²q = 0.

Получим:

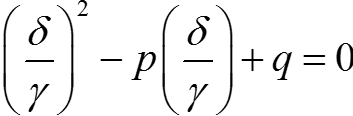
Но уравнение x² + px + q = 0 имеет отрицательный дискриминант, а значит последнее уравнение не имеет действительного решения, ⇒ Δ ≠ 0 ⇒ наша система имеет единственное нетривиальное решение.

Т. о. A и B существуют и определены однозначно.