Разложение дроби на элементарные
Доказательство
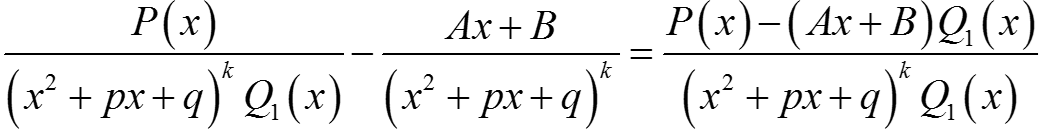 .
.
Покажем, что A и B можно подобрать так, чтобы числитель правой части делился на x2 + px + q. Продолжая последнее равенство
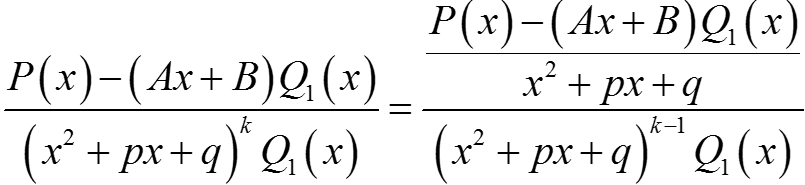
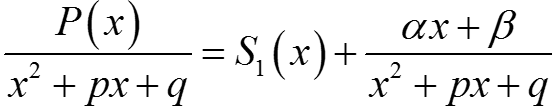
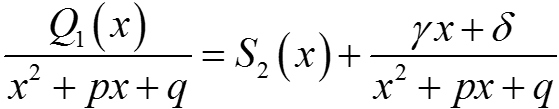
S1 и S2 — многочлены, γ2 + δ2 > 0 (иначе Q1(x) делится на x2 + px + q).
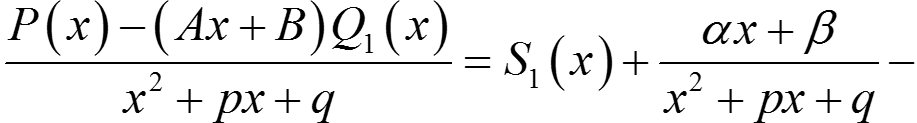
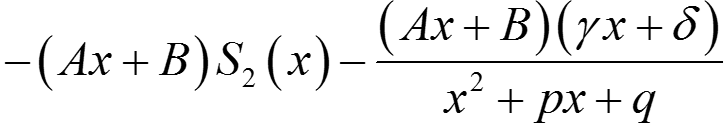 .
.

 Интегрирование рациональных выражений. Интегрирование иррациональных выражений
Интегрирование рациональных выражений. Интегрирование иррациональных выражений  Разложение дроби на элементарные
Разложение дроби на элементарные
Доказательство
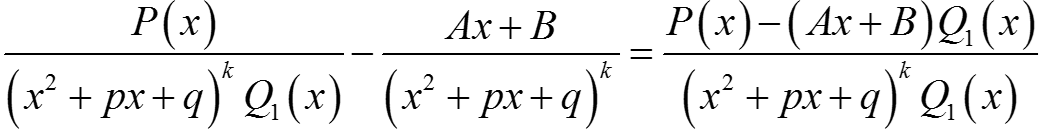 .
.
Покажем, что A и B можно подобрать так, чтобы числитель правой части делился на x2 + px + q. Продолжая последнее равенство
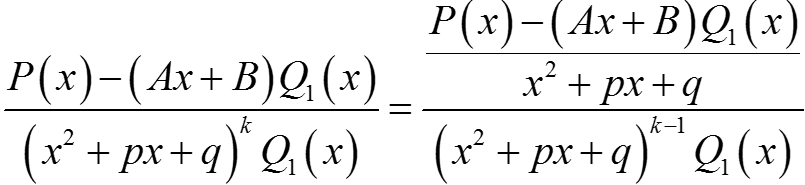
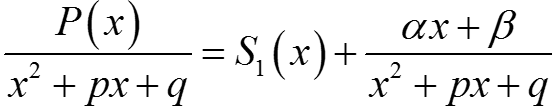
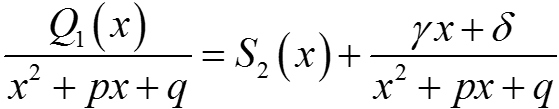
S1 и S2 — многочлены, γ2 + δ2 > 0 (иначе Q1(x) делится на x2 + px + q).
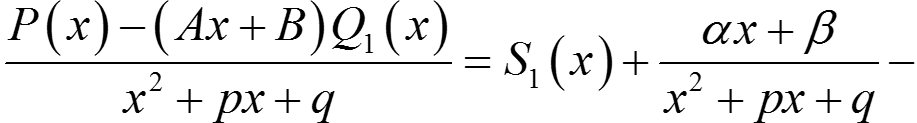
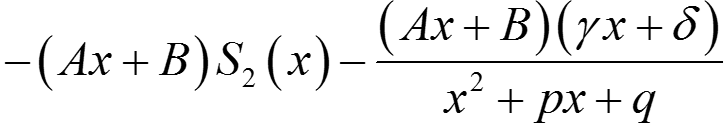 .
.