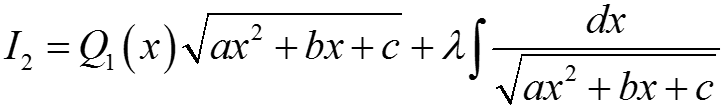Интегрирование квадратичных иррациональностей
Проинтегрировав последнее выражение и обозначив 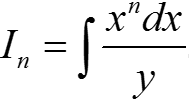 , получим рекуррентную формулу
, получим рекуррентную формулу
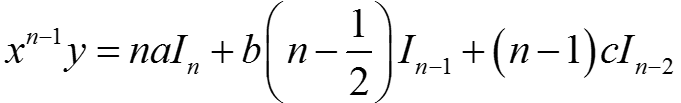 ⇒
⇒
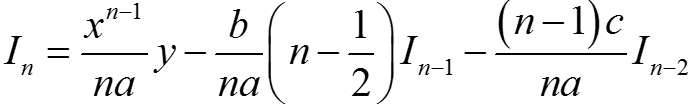
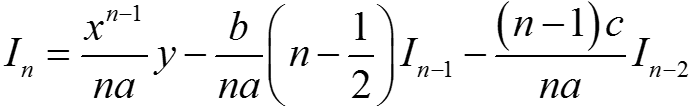
n = 1: 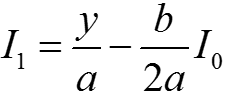
n = 2: 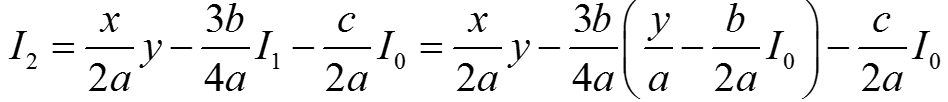 ⇒
⇒
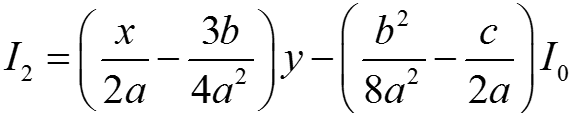 или
или
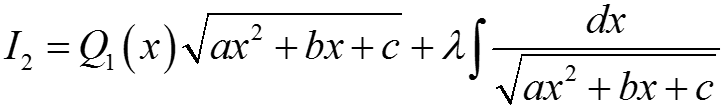

 Интегрирование иррациональных выражений. Интегрирование тригонометрических выражений
Интегрирование иррациональных выражений. Интегрирование тригонометрических выражений  Интегрирование квадратичных иррациональностей
Интегрирование квадратичных иррациональностейПроинтегрировав последнее выражение и обозначив 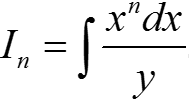 , получим рекуррентную формулу
, получим рекуррентную формулу
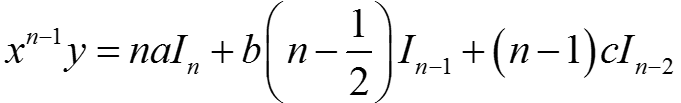 ⇒
⇒
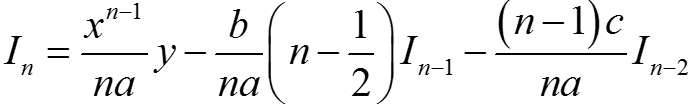
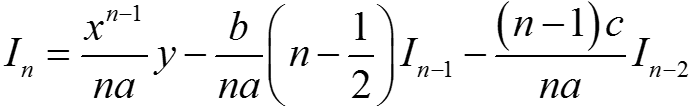
n = 1: 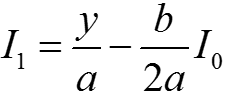
n = 2: 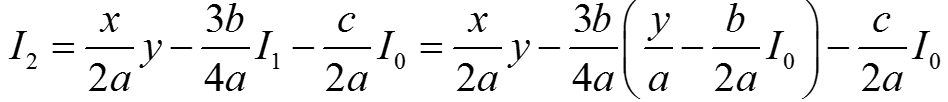 ⇒
⇒
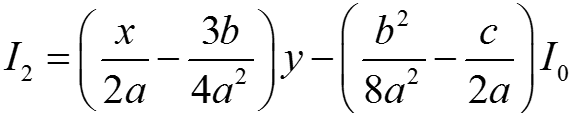 или
или