Интегрирование квадратичных иррациональностей

Последовательно переходя от I₂ к I₃, I₄ и т. д., получаем:

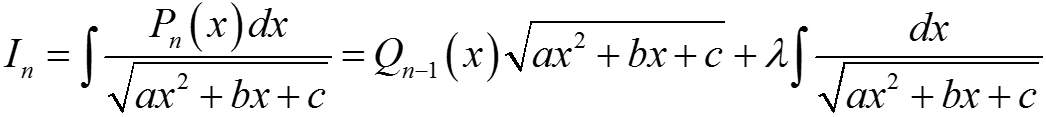где Q_n–1(x) — многочлен n − 1 — степени, λ = const. Записав Q_n–1(x) с неопределёнными коэффициентами, λ — как неопределённое число, продифференцировав (∗) и приравняв коэффициенты при одинаковых степенях x, найдём значения неопределённых коэффициентов, а значит и Q_n–1(x) и λ.

1850

Доказать, что если

y = ax² + bx + c (a ≠ 0),

то

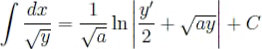при a > 0

и

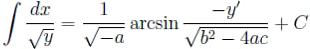при a < 0.