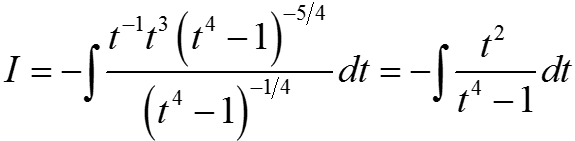Интегрирование биноминальных дифференциалов
Подстановки Чебышева
Пусть дан интеграл вида: I = ∫ xm(a + bxn)pdx.
3. ![]() + p ∈ Z, (b + ax−n) = ts, где s — знаменатель дроби
+ p ∈ Z, (b + ax−n) = ts, где s — знаменатель дроби ![]() .
.
Пример
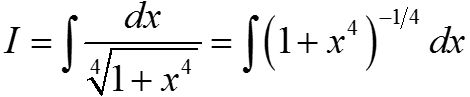
![]() ⇒ 1 + x−4 = t4 ⇒ x−4 = t4 − 1 ⇒ x = (t4 − 1)−1/4;
⇒ 1 + x−4 = t4 ⇒ x−4 = t4 − 1 ⇒ x = (t4 − 1)−1/4;
![]() ;
; ![]()
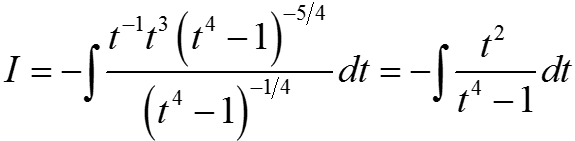

 Интегрирование иррациональных выражений. Интегрирование тригонометрических выражений
Интегрирование иррациональных выражений. Интегрирование тригонометрических выражений  Интегрирование биноминальных дифференциалов
Интегрирование биноминальных дифференциаловПодстановки Чебышева
Пусть дан интеграл вида: I = ∫ xm(a + bxn)pdx.
3. ![]() + p ∈ Z, (b + ax−n) = ts, где s — знаменатель дроби
+ p ∈ Z, (b + ax−n) = ts, где s — знаменатель дроби ![]() .
.
Пример
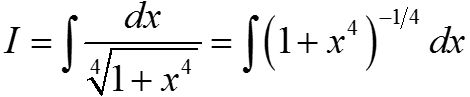
![]() ⇒ 1 + x−4 = t4 ⇒ x−4 = t4 − 1 ⇒ x = (t4 − 1)−1/4;
⇒ 1 + x−4 = t4 ⇒ x−4 = t4 − 1 ⇒ x = (t4 − 1)−1/4;
![]() ;
; ![]()