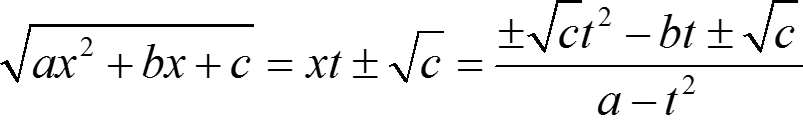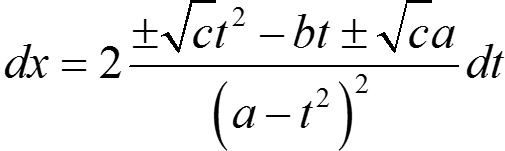Подстановки Эйлера. Пример
Интегрирование выражений вида
![]() .
.
Пусть дан интеграл вида ![]() .
.
3. c > 0 ⇒ ![]() = xt ±
= xt ± ![]() ⇒
⇒
ax2 + bx + c = t2x2 ± 2t![]() xt + c ⇒
xt + c ⇒
x(a −t2) = ±2![]() t − b ⇒
t − b ⇒ 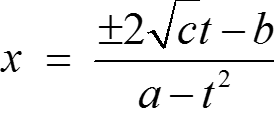
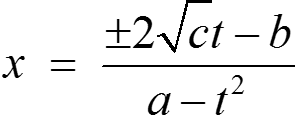 ⇒
⇒ 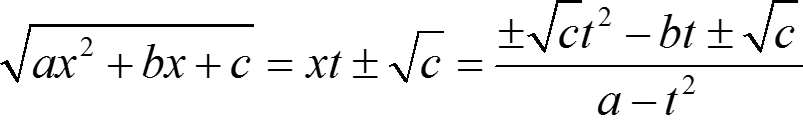
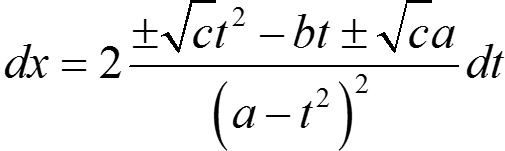

 Интегрирование иррациональных выражений. Интегрирование тригонометрических выражений
Интегрирование иррациональных выражений. Интегрирование тригонометрических выражений  Подстановки Эйлера. Пример
Подстановки Эйлера. ПримерИнтегрирование выражений вида
![]() .
.
Пусть дан интеграл вида ![]() .
.
3. c > 0 ⇒ ![]() = xt ±
= xt ± ![]() ⇒
⇒
ax2 + bx + c = t2x2 ± 2t![]() xt + c ⇒
xt + c ⇒
x(a −t2) = ±2![]() t − b ⇒
t − b ⇒ 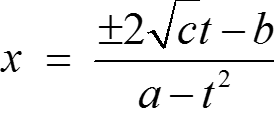
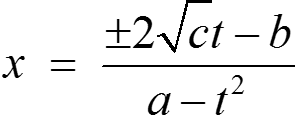 ⇒
⇒