Теорема о нуле интеграла
Теорема
Если функция y = f(x) ≥ 0 кусочно-непрерывна на отрезке [a; b] и 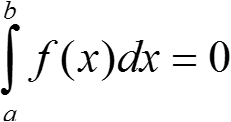 , то f(x) ≡ 0 за исключением конечного числа точек.
, то f(x) ≡ 0 за исключением конечного числа точек.
Доказательство
Если f(x0) > 0 и x0 — точка непрерывности, то f(x) > 0 ∀ x ∈ Uδ(x0) → 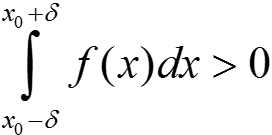 →
→ 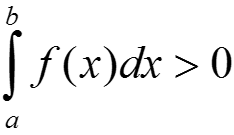 .
.
Теорема
Если функция y = f(x) ≥ 0 кусочно-непрерывна на отрезке [a; b] и 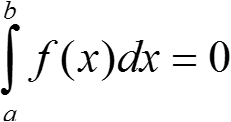 , то f(x) ≡ 0 за исключением конечного числа точек.
, то f(x) ≡ 0 за исключением конечного числа точек.
Доказательство
Если f(x0) > 0 и x0 — точка непрерывности, то f(x) > 0 ∀ x ∈ Uδ(x0) → 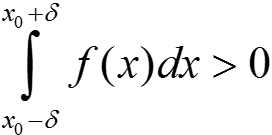 →
→ 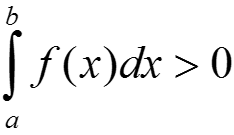 .
.