Достаточное условие интегрируемости

Пример

Функция, не имеющая интеграла

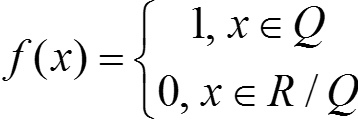
Теорема

Достаточные условия интегрируемости

Всякая непрерывная на отрезке [a; b] функция интегрируема на этом отрезке.

Доказательство

Из равномерной непрерывности функции y = f(x) следует, что .

При переходе к пределу в неравенстве (6), получим: .