Замена переменной в интеграле Римана

Рассмотрим интеграл 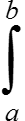f(u)du, где f(u) — непрерывная функция на отрезке [a; b].

Произведена замена переменной u = u(t), где u(t) — функция, имеющая непрерывную производную на отрезке [α; β], причём

u(α) = a, u(β) = b.

Теорема

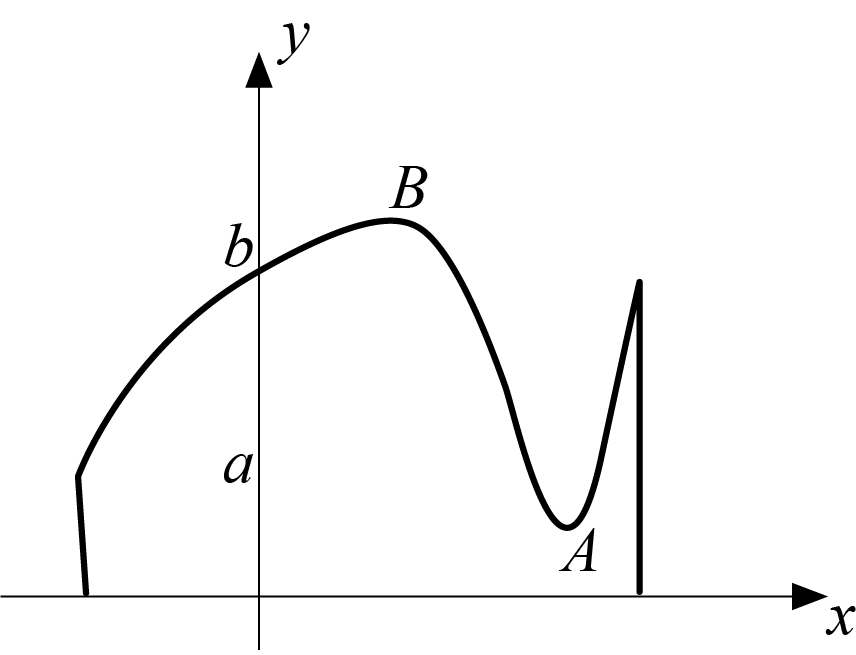
Если u = u(t) [α; β] → [A; B] ⊃ [a; b] и f(u) непрерывна на [A; B], то

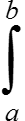f(u)du = 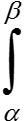f(u(t))u′(t)dt.

Доказательство

По теореме о замене переменной в неопределённом интеграле функция F(u(t)) является первообразной функции f(u(t))·u′(t) и F(u(t)) = G(t) + C, где G(t) — первообразная функции f(u(t))·u′(t). Тогда

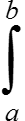f(u)du = F(b) − F(a) = F(u(β)) −F(u(α)) = G(β) − G(α) = 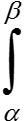f(u(t))u′(t)dt.