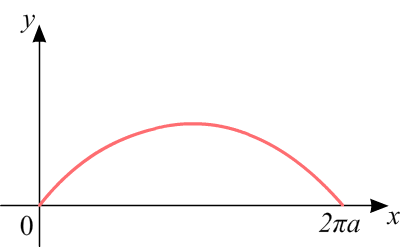
Длина кривой, заданной параметрически

Пример 8

Найти длину арки циклоиды: ,   t ∈ [0; 2π) (x′(t))2 + (y′(t))2 = a2(1 − cos t)2 + a2sin2 t = = a2(1 − 2cos t + cos2 t + sin2 t) = 4a2 sin2 .

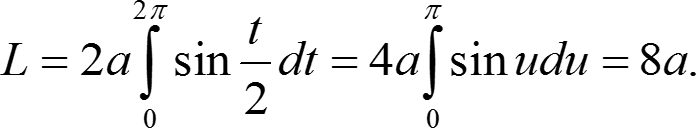
Длина кривой в полярной системе:

Уравнение кривой в полярной системе: r = r(φ), φ ∈ [φ₁; φ₂].

Параметрическая форма: 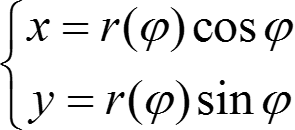, φ ∈ [φ₁; φ₂].

x′(φ) = r′ cos φ − r sin φ, y′(φ) = r′ sin φ + r cos φ,

(x′)² + (y′)² = (r′)²(cos² φ + sin² φ) + r²(cos² φ + sin² φ) = (r′(φ))² + r²(φ).
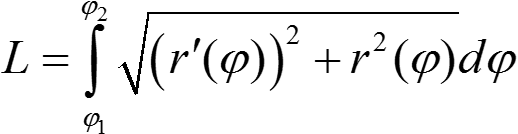
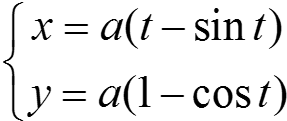