Признаки абсолютной сходимости для несобственных интегралов первого рода

2. Пусть интеграл

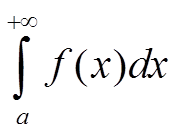
расходится, тогда по критерию Коши

∀ ε > 0 ∀ b > a: ∃ b′ > b, ∃ b′′ > b: 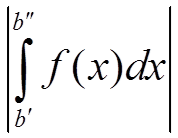≥ ε

Тогда из заданного в условии неравенства следует, что

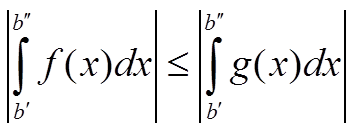
и для функции g(x) можно записать, что

∀ ε > 0 ∀ b > a: ∃ b′ > b, ∃ b′′ > b: 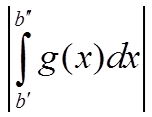≥ ε

То есть по критерию Коши интеграл

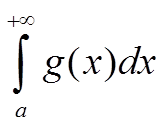
расходится.