Признаки абсолютной сходимости для несобственных интегралов первого рода

Указанную теорему можно доказать другим способом, более наглядным. Если

0 ≤ f(x) ≤ g(x), x ∈ [a, +∞)

то рассмотрим их интегралы с переменным верхним пределом

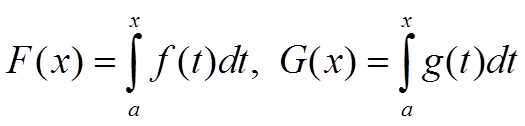
Эти интегралы являются положительными монотонно неубывающими функциями. Для неубывающих функций верна теорема:

F(x) ∈ R ⇔ F(x) — ограничена

Если ограничена большая функция G(x), то ограничена и меньшая F(x), и значит из сходимости интеграла для g(x) следует сходимость для f(x).

И, наоборот, из неограниченного возрастания меньшей функции F(x) следует неограниченное возрастание большей функции G(x), и значит из расходимости интеграла для f(x) следует расходимость для g(x).

Теорема доказана