Критерий Коши сходимости несобственного интеграла первого рода

Для сходимости несобственного интеграла

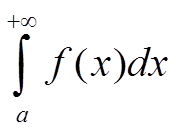
необходимо и достаточно, чтобы

∀ ε > 0 ∃ b = b(ε) > a: ∀ b′ > b, ∀ b′′ > b ⇒ 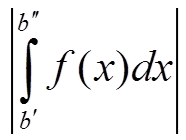< ε

Доказательство

По определению несобственный интеграл (1) сходится тогда и только тогда, когда существует конечный предел функции

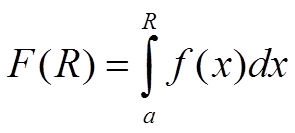
при R → +∞

По критерию Коши существования конечного предела функции необходимо и достаточно, чтобы

∀ ε > 0 ∃ b = b(ε) > a: ∀ b′ > b, ∀ b′′ > b ⇒ |F(b′′) − F(b′)| < ε

Подставим выражение для F(R) и получим

∀ ε > 0 ∃ b = b(ε) > a: ∀ b′ > b, ∀ b′′ > b ⇒ 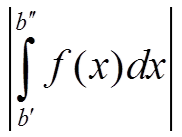< ε

Таким образом сходимость несобственного интеграла будет тогда и только тогда, когда существует конечный предел функции F(R), что и даёт условие Коши.