Примеры

Докажем, что интеграл расходится по критерию Коши. Запишем отрицание сходимости по критерию Коши.

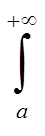f(x)dx расходится

⇔ ∃ ε > 0 ∀ b > a ∃ b′ ≥ b, ∃ b′′ ≥ b: 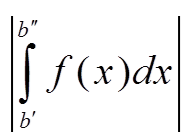≥ ε

Будем доказывать расходимость интеграла, выберем

ε = 1, ∀ b > a ∃ b₁ = [b] + 1, b₁ ∈ N, b₁ ≥ b, b₁ ≥ 1

∃ b′ = π( + 2b₁) > b, ∃ b′′ = π( + 2b₁) > b:

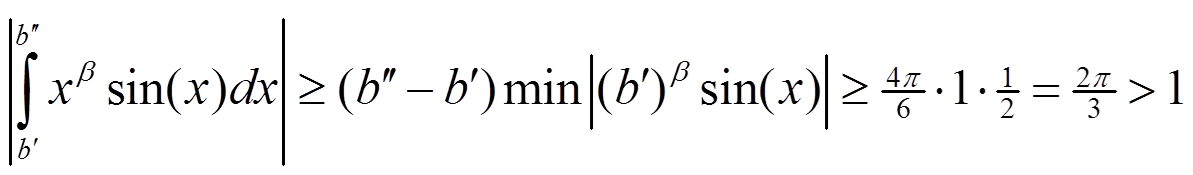
Итак, интеграл расходится по критерию Коши при α < 0.

Ответ

Интеграл 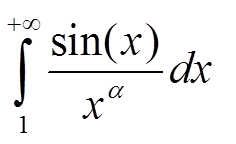расходится при α ≤ 0.

Интеграл сходится условно при 0 < α ≤ 1.

Интеграл сходится абсолютно при α > 1.