Критерий Коши измеримости. Свойства меры. Интеграл Римана.
Пример непосредственного вычисления интеграла

Свойства меры

В рассмотренных примерах

1)

2)

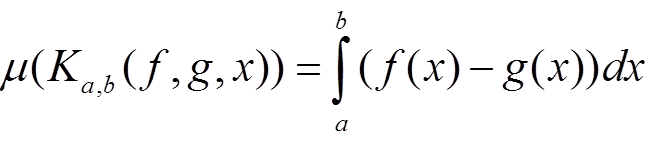
Свойства

1.

2. Если области G₁ и G₂ измеримы и G₁ ⊂ G₂, то

3. Если G измеримая область, то .

Доказательство

: области — вписанная и описанная ступенчатые области и

4. Если области G₁ и G₂ измеримы и пересекаются по границе, то

5. Если области G₁ и G₂ измеримы, то измеримы и и