Критерий Коши и признак Вейерштрасса

Пример

Исследуем на равномерную сходимость функциональный ряд: 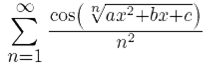на промежутке x ∈ (−∞, +∞). Легко заметить, что ∀ x ∈  выполнено неравенство

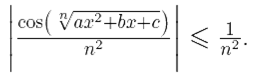
Так как числовой ряд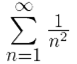сходится (по интегральному признаку), то признак Вейерштрасса гарантирует нам, что функциональный ряд 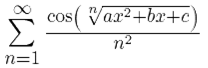сходится равномерно на (независимо от значений параметров a, b и c).