Критерий Коши и признак Вейерштрасса

Следствие

Необходимое условие равномерной сходимости

Условие

Ряд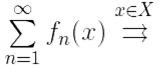сходится равномерно на X.

Утверждение

Функциональная последовательность

Доказательство

Напишем условие критерия Коши равномерной сходимости ряда и возьмем в нём p = 1:

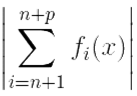∀ ε > 0   ∃ N ∈ :   ∀ n > N   для p = 1,   ∀ x ∈ X    < ε

Последнее неравенство при p = 1 имеет вид: |f_n+1| < ε. То есть, из критерия Коши следует:

 

∀ ε > 0   ∃ N ∈ :   ∀ n > N   ∀ x ∈ X   | f_n+1(x)| < ε

Но эта формула является определением равномерной на множестве X сходимости функциональной последовательности {f_n} к функции, равной тождественному нулю.