Критерий Коши и признак Вейерштрасса

Доказательство

Так как числовой ряд 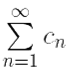сходится, то по критерию Коши для числовых рядов

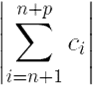∀ ε > 0   ∃ N(ε) ∈ :   ∀ n > N    ∀ p ∈ N    < ε

Это означает, в силу неравенства 0 ≤ |f_i(x)| ≤ c_i, что для того же N(ε)

∀ x ∈ X 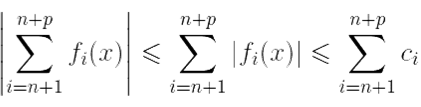    < ε

Откуда по критерию Коши ряд сходится равномерно на X, то есть

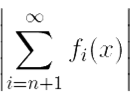∀ ε > 0   ∃ N(ε) ∈ :   ∀ n > N    ∀ x ∈ X    < ε