Критерий Коши и признак Вейерштрасса

Теорема

Критерии Коши равномерной сходимости ряда

Утверждение

Функциональный ряд сходится равномерно на множестве X.

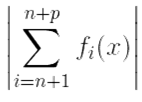⇔   ∀ ε > 0   ∃ N ∈ :   ∀ n > N   ∀ p ∈    ∀ x ∈ X    < ε

Теорема

Признак Вейерштрасса

Условие

  ∃ n ∈     ∀ x ∈ X  | f_n(x)| ≤ c_n и числовой ряд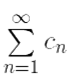сходится.

Утверждение

Функциональный ряд сходится равномерно на X.