Равномерно сходящиеся ряды

б) В отличие от пунктa а), сумма ряда непрерывна в рассматриваемой области, включая граничные точки. Проверим наличие равномерной сходимости на промежутке [0, 1 – α]. Запишем определения равномерной сходимости:

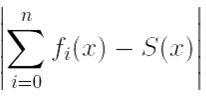∃ ε > 0:   ∃ N ∈ :   ∀ n > N   ∀ x ∈ X:    < ε

Распишем последнее неравенство:

   ≥

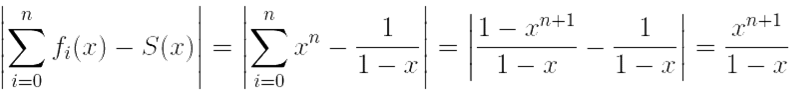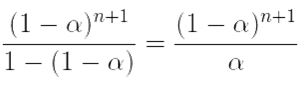 ≥   < ε

Таким образом, чтобы выполнялось последнее неравенство, нам достаточно для произвольного ε > 0 взять номер    чтобы для любого n > N и произвольной точки x ∈ [0, 1 − α] выполнялось неравенство

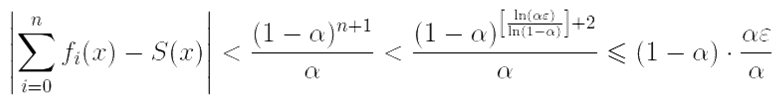< ε

то есть выполено определение равномерной сходимости ряда на промежутке [0, 1 − α].