Равномерно сходящиеся ряды

а) Разрывность предельной функции в точке x = 1 вызывает подозрение, что равномерной сходимости на промежутке [0, 1) нет. Убедимся в этом. Запишем отрицание определения равномерной сходимости:

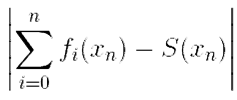∃ ε > 0:   ∀ N ∈ :   ∃ n > N   ∃ x_n ∈ X:   ≥ ε

Распишем последнее неравенство для $$\left | \sum_{i=0}^{n} f_i(x_n) - S(x_n) \right | = \left | \sum_{i=0}^{n} x_n^i - \frac{1}{1 - x_n} \right | = \left | \frac{1 -x_n^{n+1}}{1 - x_n} - \frac{1}{1 - x_n} \right | = \frac{x_n^{n+1}}{1 - x_n} > x_n^{n+1} = \frac{1}{2} \geq \varepsilon $$

 

Таким образом, для и любого N ∈ можно указать n > N (например, n = N + 1) и 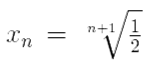такие, что

 

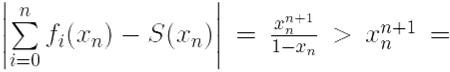
то есть выполнено определение отрицания равномерной сходимости ряда на [0, 1).