Равномерно сходящиеся ряды

Определение 2

Последовательность {f_n(x)} мы будем называть равномерно сходящейся на множестве X к функции F(x) (это обозначается 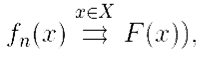если

∀ ε > 0   ∃ N ∈ : ∀ n > N   ∀x ∈ X   |f_n(x) − F (x)| < ε.

Ряд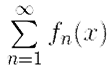 мы будем называть равномерно сходящимся на множестве X к функции S(x) (обозначается 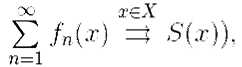если последовательность частичных сумм сходится к S(x) равномерно на X, т. е.

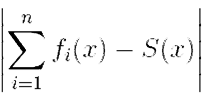∀ ε > 0   ∃ N ∈ : ∀ n > N   ∀x ∈ X    < ε

Пример

Исследовать на равномерную сходимость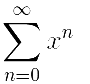

а) на промежутке [0, 1);

б) на промежутке [0, 1 − α] для произвольного α ∈ (0, 1).

Как мы выяснили

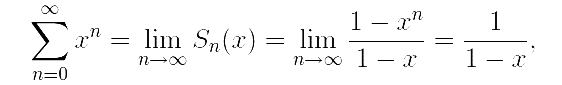|x| < 1.