Функциональные последовательности и ряды. Основные понятия

Пример

Рассмотрим последовательность функций f_n(x) = xⁿ на множестве x ∈ .

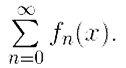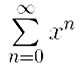Исследуем сходимость ряда Фиксируем произвольный x ∈ . Для него имеем: — числовой ряд, причём при |x| ≥ 1 ряд расходится, т. к. не выполнено необходимое условие сходимости: xⁿ 0 при n → ∞.

Осталось рассмотреть точки |x| < 1.

Для −1 < x < 0 числовой ряд 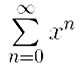является рядом Лейбница, следовательно сходится, в точке x = 0 все частичные суммы ряда равны 1, следовательно, в x = 0 ряд сходится к 1. Для 0 < x < 1 наш числовой ряд — геометрический, поэтому сходится. Чтобы выяснить, к какой функции сходится функциональный ряд на |x| < 1, вспомним формулу геометрической прогрессии, подставим в неё q = x и перейдём к пределу при n → ∞:

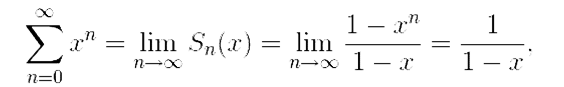|x| < 1.