Функциональные последовательности и ряды. Основные понятия

Определение 1

Функциональной последовательностью называется бесконечное занумерованное множество функций

Пределом функциональной последовательности на множестве M называется функция F(x) такая, что равенство выполнено в каждой точке x ∈ M, т. е.

∀ x ∈ M   ∀ ε > 0   ∃ N ∈ : ∀ n > N   | f_n(x) − F(x)| < ε

Функциональным рядом называется выражение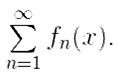

n-ой частичной суммой S_n функционального ряда 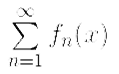называется функция

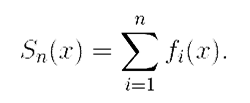
Суммой S функционального ряда 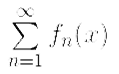называется функция — предел его частичных сумм:

eсли такой предел существует во всех точках некоторого множества M. Само множество M называется областью (поточечной) сходимости ряда, а ряд — сходящимся на M, при этом пишут x ∈ M.