Свойства равномерно сходящихся рядов. Почленный переход к пределу

Следствие

О непрерывности суммы

Условие

сходится равномерно на множестве X к сумме S(x) при этом функции f_n(x) непрерывны в точке a ∈ X.

Утверждение

S(x) непрерывна в точке a.

Доказательство

Пусть функции f_n(x) непрерывны в точке a ∈ X. Это означает, что

∀ n ∈    

По теореме о почленном переходе в равномерно сходящихся рядах, получим:

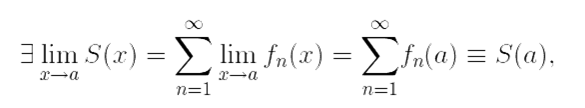
То есть, функция S(x) непрерывна в точке a.