Почленное интегрирование и почленное дифференцирование
Теорема
Почленное дифференцирование
Условие
Все функции fn(x) имеют производные на [a, b] и
1) ряд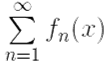 
сходится хотя бы в одной точке с ∈ [a, b];
2) ряд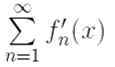 
сходится равномерно на [a, b].
Утверждение
1) ряд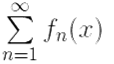 
сходится равномерно на [a, b] к некоторой функции S(x);
2) 
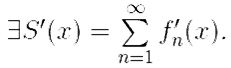
Замечание
Приведённые свойства равномерно сходящихся рядов говорят о том, что такие ряды очень удобны в обращении: с ними можно почленно выполнять самые важные операции: переход к пределу, интегрирование и дифференцирование, поэтому если удастся найти класс рядов, которые сходятся равномерно, то этот класс становится удобным инструментом математического исследования. Такие классы (степенные ряды (и, в частности, ряд Тейлора) и ряды Фурье) мы опишем в следующих параграфах.
Замечание
Теоремы о свойствах равномерно сходящихся рядов переписываются с соответствующими изменениями для равномерно сходящихся функциональных последовательностей.
