Теорема о единственности разложения функции в степенной ряд

Теперь подставим в полученные равенства x = a (по теореме о непрерывности суммы степенного ряда) мы имеем право подставить x = a в выражения под знаком ряда. Получим:

f(a) = c₀,

f '(a) = 1 · c₁,

f ''(a) = 1·2 · c₂,

f '''(a) = 1·2·3 · c₃,

f ^k(a) = 1·2 · ... k · c_k = k! · c_k,

Отсюда для коэффициентов c_n ряда (8.3) имеем равенство:

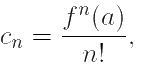       n = 0, 1, 2, ...

Таким образом, если функция имеет производные любого порядка и разлагается в степенной ряд в (a − R, a + R), то коэффициенты этого ряда определяются единственным образом по формуле