Достаточное условие разложимости
Достаточное условие разложимости
Пусть в интервале (a − δ; a + δ) с некоторыми постоянными С и b выполнены неравенства
| f (n)(x) | ≤ Cbn n!
Тогда функция f(x) разложима в ряд Тейлора в интервале (a − δ1; a + δ1), где δ1 = min (δ, 1/b). $$f(x) = \sum_{k=0}^{n} \frac{f^{(n)}(a)}{n!} (x - a)^n + \frac{f^{(n+1)}(\xi)}{(n+1)!} (x - a)^{n+1}$$ $$f(x) = \sum_{k=0}^{\infty} \frac{f^{(n)}(a)}{n!} (x - a)^n \Leftrightarrow \lim_{n \rightarrow \infty} \frac{f^{(n+1)}(\xi)}{(n+1)!} (x - a)^{n+1} = 0$$
Замечание: xn → x ⇔ xn+1 → x
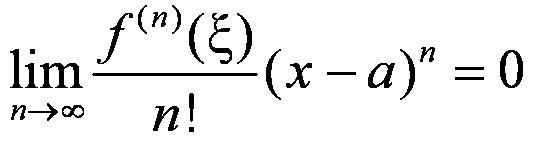
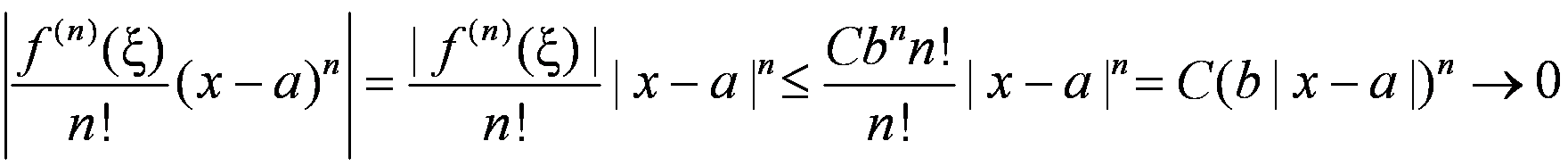
(если только b |x − a| < 1, т. е. |x − a| < 1/b)



