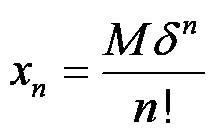Достаточное условие разложимости

Следствие

Пусть в интервале (a − δ; a + δ) функция f(x) бесконечно дифференцируема и в этом интервале с некоторой постоянной М при всех n выполнено неравенство

Тогда функция f(x) разложима в ряд Тейлора в этом интервале.

Достаточно показать, что выполнено неравенство

|f ⁽ⁿ⁾(x)| ≤ Cbⁿn!

при

b = 1/δ.

В этом случае

δ₁ = min (δ, 1/b) = min (δ, δ) = δ.