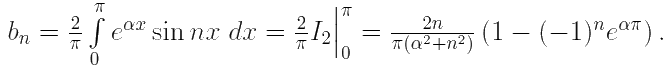Ряд Фурье «по синусам» и «по косинусам»
Поскольку тригонометрический ряд Фурье четной на [−π, π] функции содержит только слагаемые с cos nx, а нечетной — только слагаемые с sin nx, то говорят, что чётная функция разложена в ряд Фурье «по косинусам», а нечётная — «по синусам». В то же время, если нас не интересует поведение суммы нашего ряда слева от нуля (что очень часто случается в приложениях), то мы вправе рассмотреть вместо заданной функции функцию, продолженную на [−π, 0) либо чётным, либо нечётным образом. Это избавит нас от необходимости вычислять все коэффициенты общего тригонометрического ряда Фурье, т. к. достаточно будет найти только an (либо bn). Поэтому часто задачи могут быть сформулированы как в нижеследующем примере.
Пример
Разложить на промежутке [0, π] функцию f(x) = eαx в ряд Фурье
а) по синусам;
b) по косинусам. В обоих случаях нарисовать график суммы ряда.
a) Мы уже вычисляли интегралы
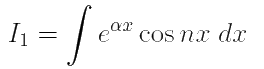 и
и 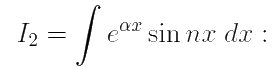
![]()
Воспользуемся этим результатом. Раз мы раскладываем по синусам, значит все an= 0, а bn вычисляются по формуле: