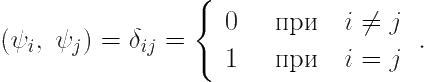Скалярное произведение. Ортонормированные системы
Рассмотрим множество всех функций, непрерывных на отрезке [−π, π]. За исключением, быть может, конечного числа точек хi разрыва I-го рода, в каждой из которых выполнено равенство
(Заметим, что в точках непрерывности функции f(x) это равенство автоматически выполняется.)
Указанное множество функций мы будем обозначать QC[−π, π].
Определение
Скалярным произведением пары f и 
элементов QC[−π, π] назовём число
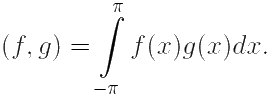
Определение
9.2. Функции f и из QC[−π, π] мы будем называть ортогональными, если (f, ) = 0.
Определение
9.3. Систему функций 
из QC[−π, π] ортортонормированной системой, если
2/15
