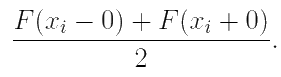Теорема о сумме ряда Фурье

Теорема

Сумма ряда Фурье

Условие

f(x), f'(x), ∈ QC[−π, π].

Утверждение

1. Ряд Фурье функции f(x), сходится к f(x), на [−π, π], при этом, на любом отрезке [a, b] ⊂ (−π, π), не содержащем точек разрыва f(x) этот ряд сходится равномерно.

2. Вне отрезка [−π, π] ряд Фурье функции f(x) сходится к её 2π-периодическому продолжению, то есть к функции, определённой по закону:

F(x) = f(x − 2πk) на любом интервале ((2k − 1)π, (2k + 1)π), k ∈ .

При этом во всех точках х_i разрыва F(x) ряд Фурье сходится к