Теорема о сумме ряда Фурье

Следствие

Условие

f(x), f '(x), ∈ QC[−π, π].

Утверждение

Ряд Фурье можно почленно интегрировать на любом отрезке [a, b] ⊂ (−π, π) не содержащем точек разрыва f(x).

Следствие

Условие

f(x), f '(x), f ''(x), ∈ QC[−π, π].

Утверждение

Ряд Фурье можно почленно дифференцировать на любом отрезке [a, b] ⊂ (−π, π) не содержащем точек разрыва
f(x) и f '(x).

Полученный ряд

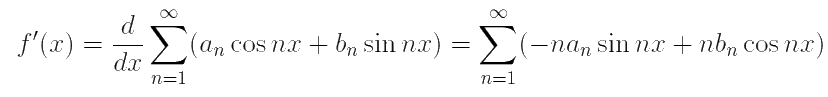
будет рядом Фурье функции f '(x) и будет сходиться к ней равномерно на [a, b] ⊂ (–π, π).