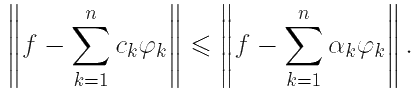Ряд Фурье в гильбертовом пространстве

Определение

Система элементов H называется полной, если для любого элемента f ∈ H существует разложение по этой системе, т. е. найдутся такие коэффициенты α_k ∈ , что

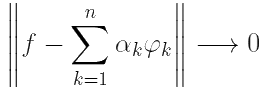   при n → ∞

Определение

Рядом Фурье для элемента f ∈ H по ортогональной системе называется ряд $$f \sim \sum_{k=1}^{\infty} c_k \varphi_k, \: \ce{где} \: c_k = \frac{(f, \varphi_k)}{||\varphi_k||^2}.$$

Числа с_k называются коэффициентами ряда Фурье.

Теорема

Минимизирующее свойство коэффициентов Фурье

Пусть H-гильбертово пространство, а — ортогональная система элементов H. Элементу f ∈ H его сопоставлен ряд Фурье с коэффициентами с_k.

Тогда для ∀ набора коэффициентов и∀ n ∈ справедливо неравенство