Ряд Фурье в гильбертовом пространстве

Итак,

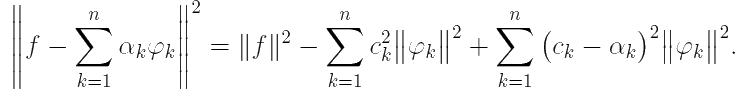
Первое и второе слагаемые правой части от набора коэффициентов никак не зависят, потому исследуем последнее:Эта сумма всегда неотрицательна и обращается в нуль тогда и только тогда, когда

\(\alpha_k = c_k\)   

Таким образом, минимального значения разностьдостигает при совпадении α_k с коэффициентами Фурье для элемента f.

Замечание

Данная теорема называется теоремой «о минимизирующем свойстве коэффициентов Фурье» и означает, что если нам нужен ряд по ортогональной системе функций, дающий наилучшее приближение к f, то наилучшим кандидатом является ряд Фурье, так как именно его частичная сумма ближе любых других линейных комбинаций {φ₁, ... φ_n} к элементу f.