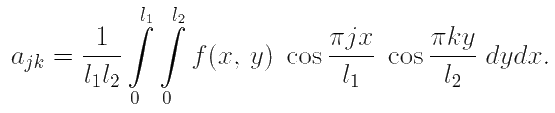Приложения методов Фурье. Ряд Фурье для аппроксимации изображений

Ряд Фурье для аппроксимации изображений

Ряды, в частности, ряды Фурье, можно использовать для аппроксимации изображений. Пусть, например, дано изображение с маленьким разрешением:

Предположим, мы хотим его увеличить в два раза, но так, чтобы гладкие линии остались гладкими, а не ступенчатыми, как при простом удвоении размеров (см. последний рисунок).

Превратим этот рисунок в сеточную функцию. Каждая точка рисунка имеет яркость, задаваемую в формате .bmp целочисленным значением от 0 до 255. Назовём полученную функцию f(x, y) и воспользуемся формулами частичных сумм двойного ряда Фурье по косинусам:

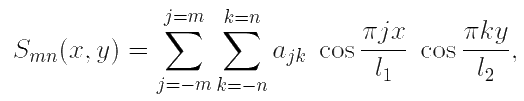
где l₁ — ширина рисунка, а l₂ — его высота (в нашем примере l₁ = l₂ = 100 пикселей), а коэффициенты a_jk находятся по формулам: