Преобразование Фурье

Тогда для функции f(x) существует косинус-преобразование Фурье:

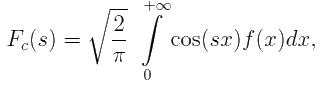
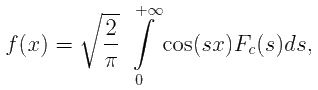   x > 0

При этом x < 0 первая часть последнего представления равна чётному продолжению f(x) на отрицательную полуось.

Аналогично, для функции f(x) существует синус-преобразование Фурье:

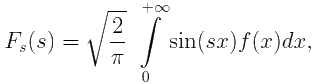
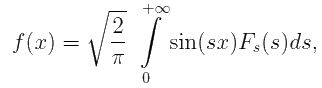x > 0

При этом для x < 0 правая часть последнего представления равна нечётному продолжению f(x) на отрицательную полуось.