Формула замены переменных

Разложим функции x(u, v) и y(u, v) по формуле Тейлора в точке (u_i, v_j):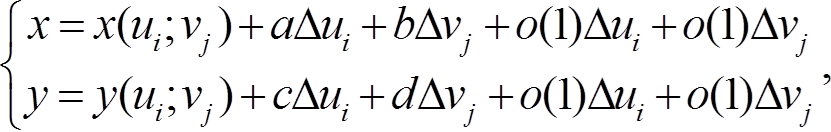

где J(u_i, v_j) = 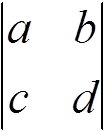— якобиан замены переменной.

Площадь образа .

Тогда

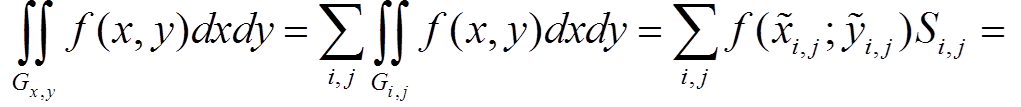
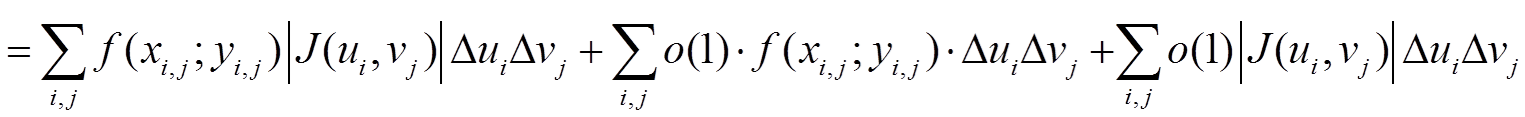
Второе и третье слагаемые стремятся к нулю, при d(ξ) → 0, поскольку функция f(x, y) и якобиан преобразования ограничены, а область _u,v измерима.

Тогда .