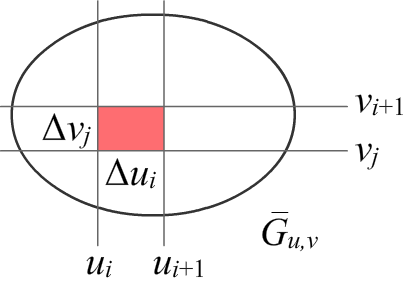
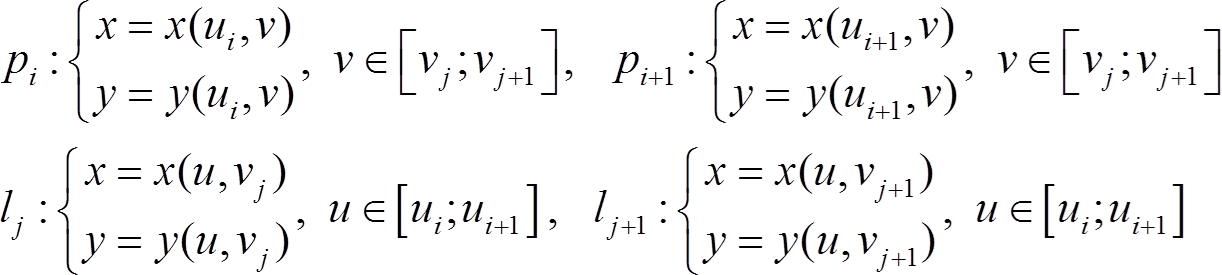Формула замены переменных

Теорема

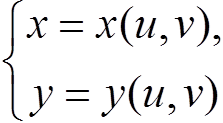Функция f(x, y) непрерывна на компакте _x,y. Замена переменных осуществляет биективное отображение компакта _u,v и переводит ∂_u,v в ∂_x,y. Функции x(u, v) и y(u, v) имеют непрерывные частные производные в _u,v. Тогда имеет место равенство:

где |J(u, v)| — модуль якобиана замены.

Доказательство