Формула Грина

Теорема

Пусть функции P(x, y) и Q(x, y) непрерывно дифференцируемы в области D. Пусть область G целиком лежит в D. Тогда справедлива формула Грина:

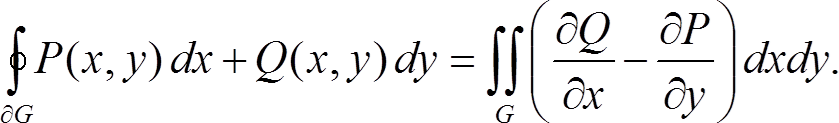
Интеграл левой части берётся по границе области в положительном направлении (т. е. при таком направлении обхода, при котором область всё время остаётся слева).

Замечание

Данная теорема очень полезна, поскольку связывает объекты разной природы — криволинейный интеграл по замкнутому контуру и двойной интеграл по области. Таких взаимосвязей в математике довольно много и все они чрезвычайно полезны, так как позволяют выбирать, каким из равных выражений удобнее воспользоваться в каждом конкретном случае.