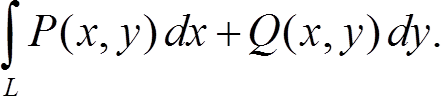Криволинейные интегралы. Основные определения

Пусть теперь в каждой точке кривой заданы непрерывные функции

f(x, y), P(x, y), Q(x, y)

Выражения

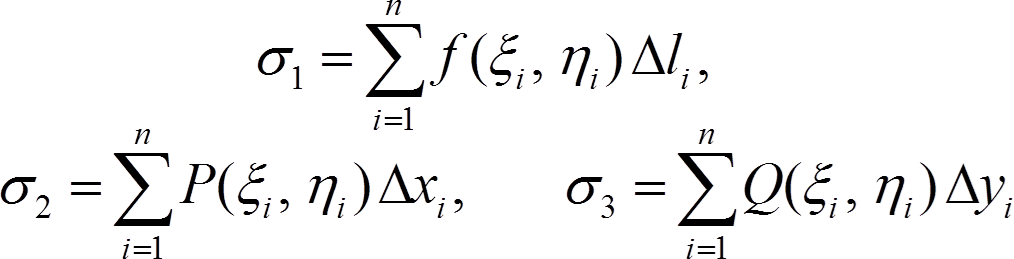
Мы будем называть первой, второй и третьей интегральной суммой, соответственно.

Если теперь рассмотреть всевозможные разбиения отрезка на частичные отрезки и всевозможные способы выбора произвольных точек

τ_i ∈ [t_i−1, t_i]

и устремить диаметр разбиения к нулю (т. е. рассматривать только разбиения со всё меньшим диаметром), то интегральные суммы будут стремиться к своим пределам, которые мы будем называть криволинейным интегралом первого и второго рода, соответственно, и обозначать:

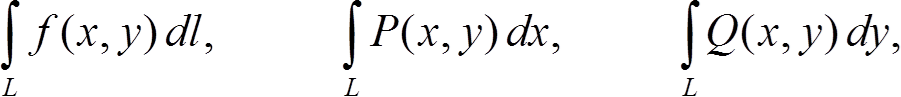
причём сумму двух последних интегралов называют общим криволинейным интегралом второго рода и обозначают