Условие на координаты векторного поля для его потенциальности. Необходимое и достаточное условие потенциальности
2) Достаточное условие потенциальности: если непрерывно дифференцируемое векторное поле
![]()
в односвязной области удовлетворяет условию
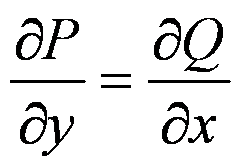
то оно потенциально.
Для доказательства проверим первое условие потенциальности поля. Пусть L — замкнутая кривая, а Ω — область, которую она ограничивает, тогда по формуле Грина
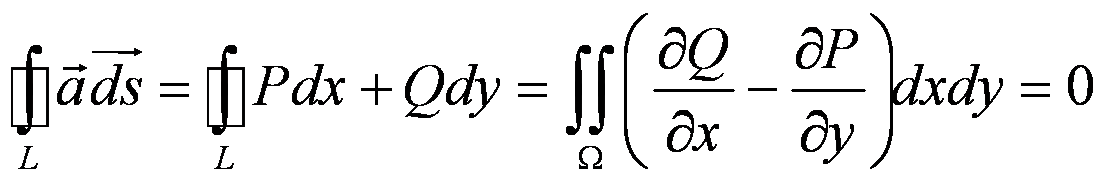
Если область в которой задано поле не односвязно, то условие
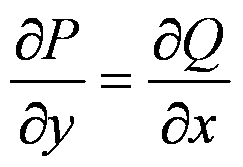
не достаточно для потенциальности поля.



