Условие на координаты векторного поля для его потенциальности. Необходимое и достаточное условие потенциальности

Условие на координаты векторного поля для его потенциальности

1) Необходимое условие потенциальности: если непрерывно

является потенциальным, то

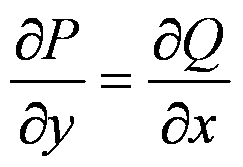
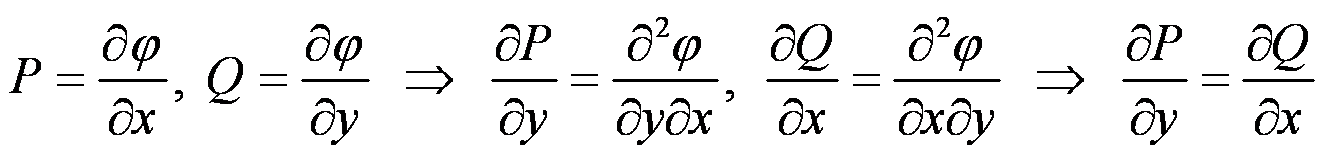
Определение

Область D называется односвязной если для любой замкнутой кривой L, целиком лежащей в области D, область Ω, ограниченная кривой L, также целиком лежит в области D.

не односвязная область

односвязная область