Условие на координаты векторного поля для его потенциальности. Необходимое и достаточное условие потенциальности

Определение

Область Ω в R³ называется поверхностно односвязной если любая замкнутая простая (т. е. без самопересечений) кривая является краем некоторой поверхности, целиком лежащей в Ω.

Определение

Область Ω в R³ называется (пространственно) односвязной если любая замкнутая поверхность S, лежащая в Ω, ограничивает область, целиком лежащую в Ω.

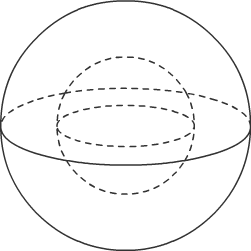
	Шар с полостью: поверхностно односвязна, но не пространственно односвязна
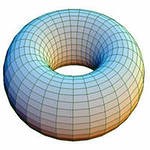
	Тор: не является поверхностно односвязным, но является пространственно односвязным