Знакочередующийся ряд. Теорема Лейбница. Оценка остатка ряда лейбницевского типа

Пусть числовой ряд сколь угодно далеко содержит как положительные, так и отрицательные слагаемые, т. е.
∀ N ∃ m > n > N : u_m · u_n < 0.Такой ряд называется знакопеременным. Важным частным случаем знакопеременного ряда является знакочередующийся ряд:

(1) v₁ − v₂ + v₃ − v₄ + ... + (−1)ⁿ⁻¹ v_n + ... = 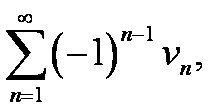где все v_n > 0.

Теорема Лейбница

Достаточный признак сходимости знакочередующегося ряда

Если последовательность {v_n} монотонно стремится к нулю, то знакочередующийся ряд (1) сходится.

Имеет место оценка остатка ряда лейбницевского типа: |r_n| = |S − S_n| < v_n+1

Доказательство

1.  S2k= (v1 − v2) + (v3 − v4) + ... (v2k−1 − v2k)     S2(k+1) = (v1 − v2) + (v3 − v4) + ... (v2k−1 − v2k) + (v2k+1 − v2k+2) =     = S2k + (v2k+1 − v2k+2) ≥ S2k ⇒ монот. неубыв., 2.  S2k = v1 − (v2 − v3) − (v4 − v5) − ... − (v2k−2 − v2k−1) − v2k ≤ v1     ⇒ ограничена сверху, 3.  S2k+1 = S2k + v2k+1⇒