Знакочередующийся ряд. Теорема Лейбница. Оценка остатка ряда лейбницевского типа
Таким образом, ![]() сходится.
сходится.
S2k+1 = v1 − (v2 − v3) −... − (v2k − v2k+1), S2(k+1)+1 = v1 − (v2 − v3) − ... − (v2k − v2k+1) − (v2k+1 − v2k+3) ≤ S2k+1 Таким образом, S2k+1 |
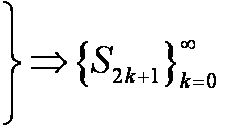 монот. невозр. монот. невозр. |
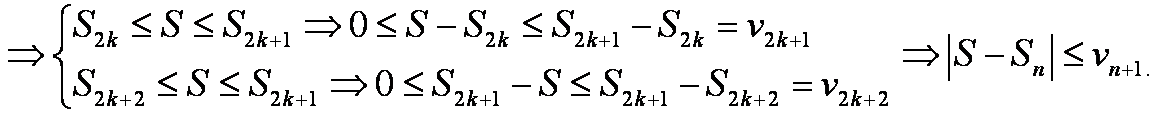
Примеры
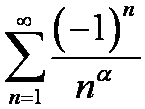 сходится при α > 0,
сходится при α > 0, 
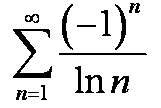 сходится т. к.
сходится т. к. 



