Абсолютно и условно сходящиеся ряды

Ряд называется абсолютно сходящимся, если сходится ряд из модулей его членов

Теорема

Если сходится ряд то ряд также сходится.

Доказательство

Ряд сходится ⇒ ⇒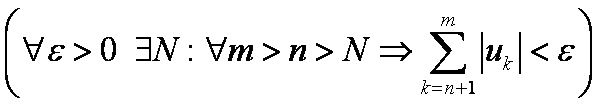

Для этих же номеров m и n имеет место ⇒ для выполнено условие Коши ⇒ ряд сходится.

Если сам сходится, а ряд расходится, то называется условно сходящимся. 

сходится абсолютно, т. к. сходится (α = 2 > 1),

сходится условно, т. к. сам он лейбницевского типа, а ряд расходится.