Монотонность в признаке Лейбница

При исследовании рядов на абсолютную сходимость можно применять все признаки, установленные  для рядов с положительными членами.

Напомним, что при доказательстве этих признаков установлено, что значение q > 1 в них свидетельствует о нарушении необходимого условия сходимости ряда. Таким образом, при q > 1 нет не только абсолютной, но даже условной сходимости, поскольку общий член ряда не стремится к нулю.

Пример

Исследовать на сходимость ряд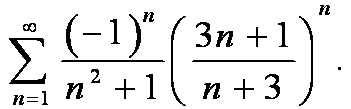

Имеем = 3 > 1. Согласно радикальному признаку Коши, модуль общего члена 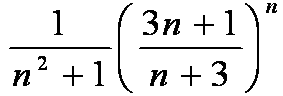не стремится к 0 ⇒ и сам он не стремится к 0 ⇒ ряд расходится.